axuhongbo的个人博客

线性方程组在实际应用中，直接进行求解有两个重大的问题：

• 计算量大，对于行星观测而言，几万、几十万观测数据轻轻松松，就算有计算机帮忙，也会面临效率问题
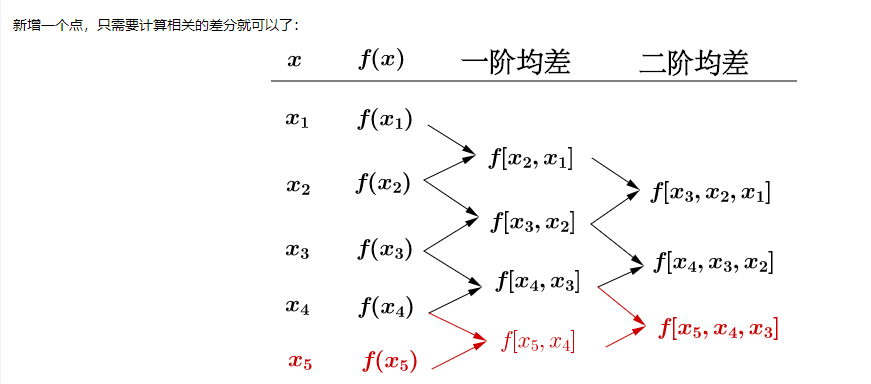
• 新增加一个点的观测数据，整个计算就要重新来过，想想就很悲伤

这里叫做牛顿插值法的几何意义不太贴切，因为若干点决定的多项式往往是唯一的（这个就是在线性代数里面的问题了），所以从几何上你看不出背后是用的牛顿插值法还是直接解线性方程组。

牛顿插值法的特点在于：每增加一个点，不会导致之前的重新计算，只需要算和新增点有关的就可以了。