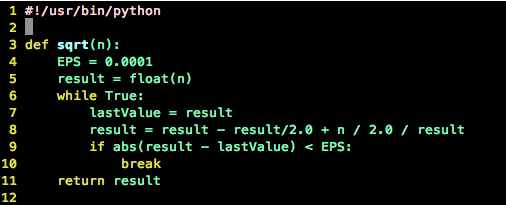
高次方程没有通解,可以依靠牛顿迭代法来求解。
五次及以上多项式方程没有根式解(就是没有像二次方程那样的万能公式),这个是被伽罗瓦用群论做出的最著名的结论。
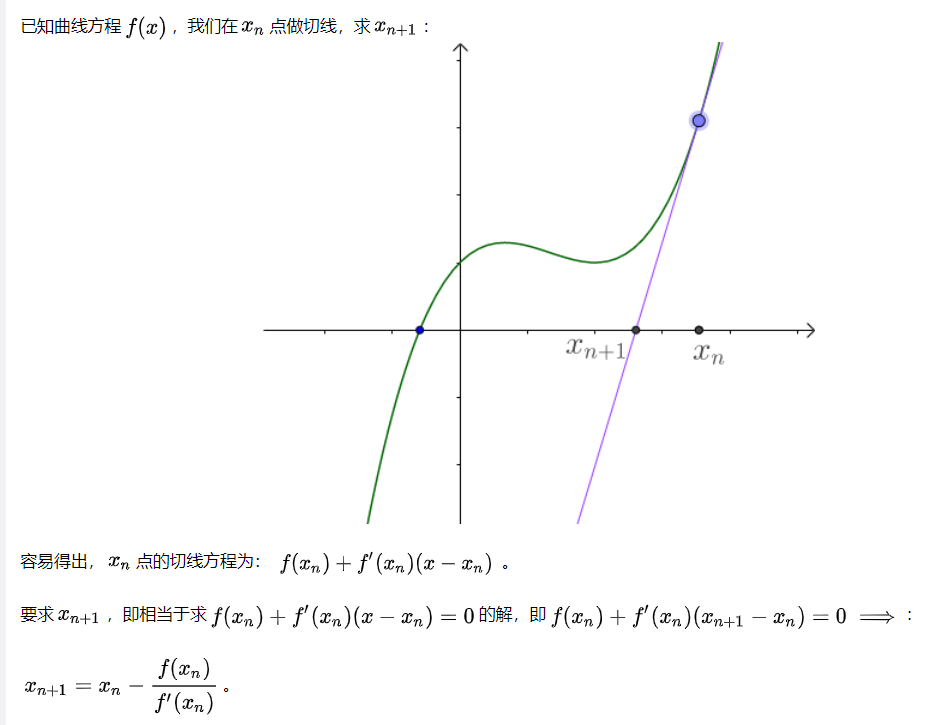
随便找一个曲线上的A点,做一个切线,切线的根(就是和x轴的交点)与曲线的根,还有一定的距离。
我们从这个切线的根出发,做一根垂线,和曲线相交于B点,继续重复刚才的工作。
经过多次迭代后会越来越接近曲线的根(下图进行了50次迭代,哪怕经过无数次迭代也只会更接近曲线的根,用数学术语来说就是,迭代收敛了)
注意 这种方法不能完整求出所有的根。
如震荡,越来越远离的不收敛等情况
与起始点的选取也有一定的关系。
应用:可以用来求解平方根
代码: