二次型就是通过矩阵研究二次函数。
一个二次方程最重要的就是二次项,改变一次项和常数不会太大的改变它的形状。
因为二次函数(方程)的二次部分最重要,为了方便研究,我们把含有n个变量的二次齐次函数:
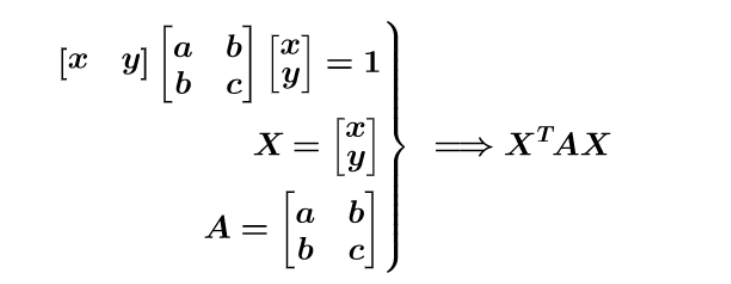
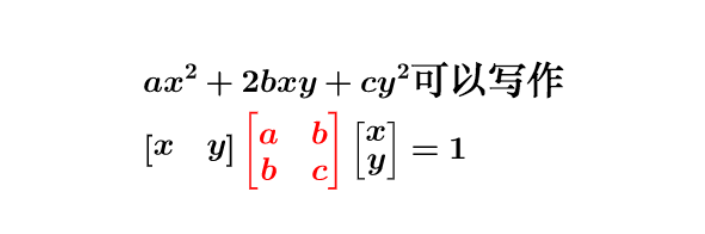
或者二次齐次方程称为二次型。
对称矩阵 = 二次型矩阵 =二次型
通过二次型我们可以发现
圆、椭圆、双曲线之间包含有线性关系,他们是 仿射的。
一个平面在圆锥体上运动,可以得到圆、椭圆、双曲线。
我们对二次型矩阵进行特征值分解,得到正交矩阵和对角矩阵
只保留表示拉伸的对角矩阵,我们就将二次型矩阵规范化
也就说说把矩阵扶正了。
正定函数值大于0
半正定函数值大于等于0
负定函数值小于0
特征值都大于0,则为正定矩阵。
傅立叶级数实际上就是把f(x)作是圆周运动的组合。
应用有图像压缩(原理大概是把基上数值特别小的数丢掉)和模式识别
