https://blog.csdn.net/txl199106/article/details/64441994
另一个很好的例子:https://blog.csdn.net/Richard__Luan/article/details/81002097
增广路算法的关键是 寻找增广路 和 改进网络流。
问题: 为什么要创建反向弧呢?
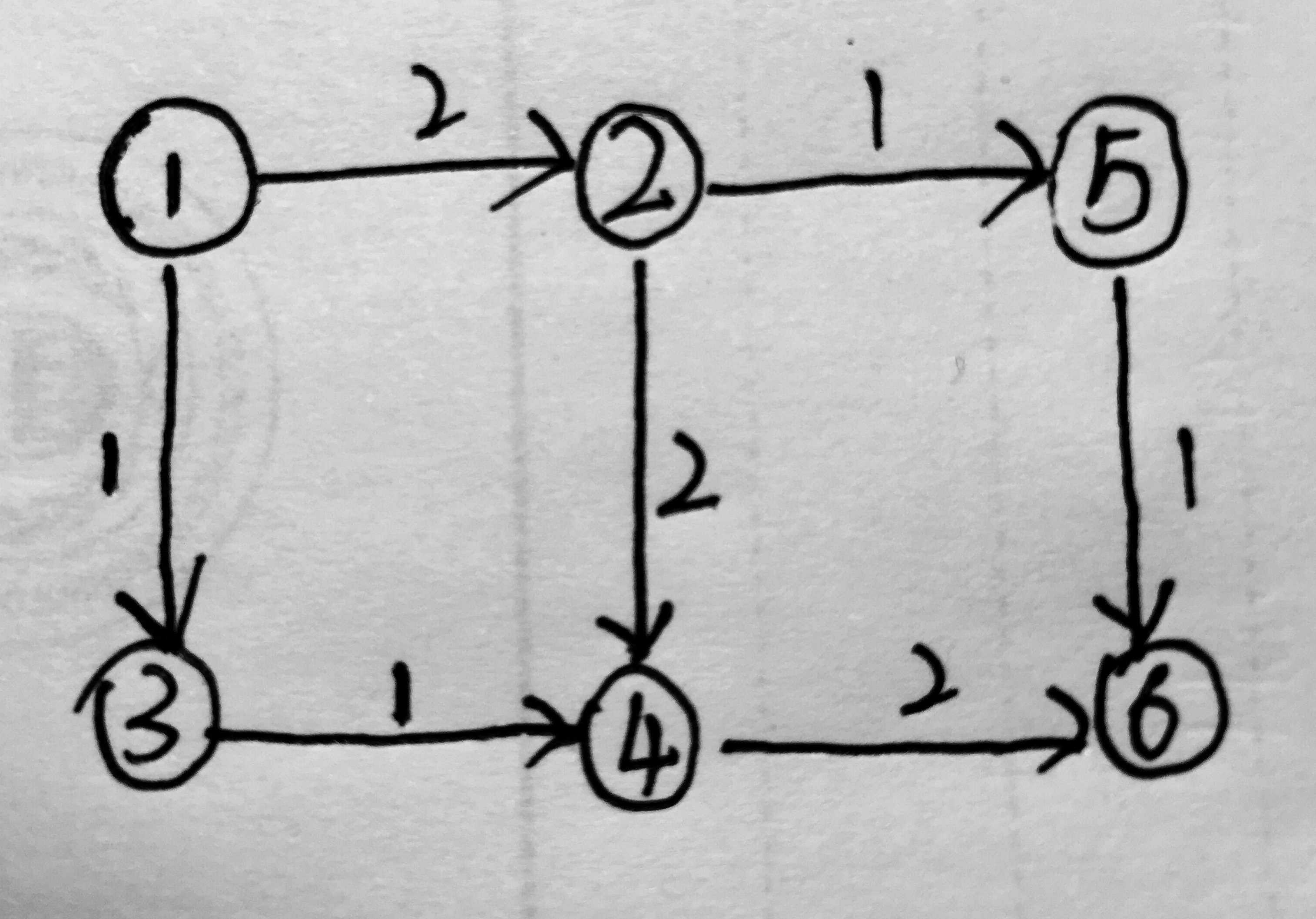
原因: 为程序提供一次反悔的机会 什么意思, 如下图所示:
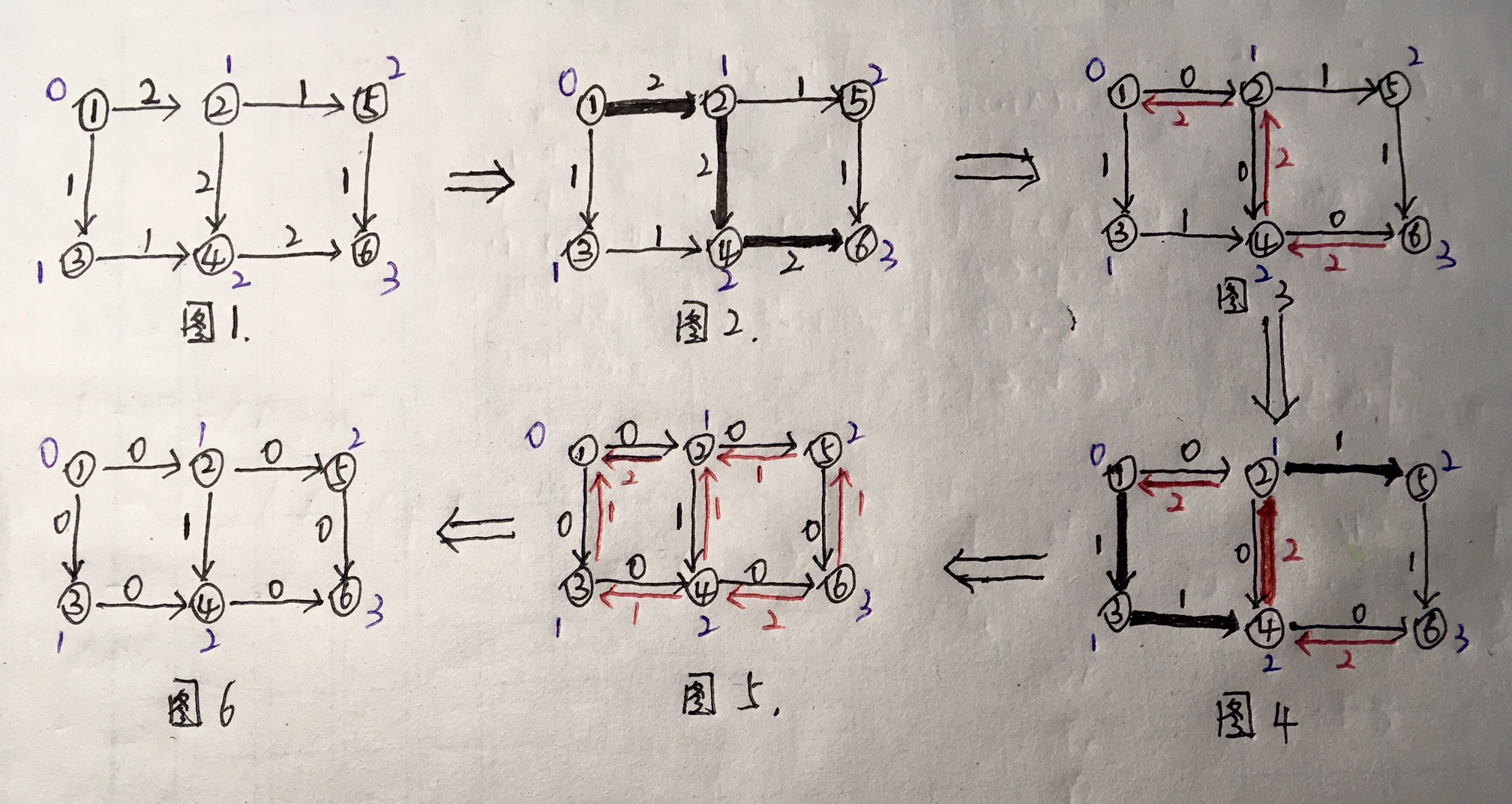
在图中如果程序找到了一条增广路 1 -> 2 -> 4 -> 6, 此时得到一个流量为 2 的流并且无法继续进行增广,
但是如果在更新可行流的同时建立反向弧的话, 就可以找到 1 -> 3 -> 4 -> 2 -> 5 -> 6 的可行流, 流量为1, 这样就可以得到最大流为 3.
Dinic 算法
算法思想
DINIC 在找增广路的时候也是找的最短增广路, 与 EK 算法不同的是 DINIC 算法并不是每次 bfs 只找一个增广路, 他会首先通过一次 bfs 为所有点添加一个标号, 构成一个层次图, 然后在层次图中寻找增广路进行更新。
算法流程
利用 BFS 对原来的图进行分层,即对每个结点进行标号, 这个标号的含义是当前结点距离源点的最短距离(假设每条边的距离都为1),注意:构建层次图的时候所走的边的残余流量必须大于0
用 DFS 寻找一条从源点到汇点的增广路, 注意: 此处寻找增广路的时候要按照层次图的顺序, 即如果将边(u, v)纳入这条增广路的话必须满足dis[u]=dis[v]−1, 其中 dis[i]为结点 ii的编号。找到一条路后要根据这条增广路径上的所有边的残余流量的最小值ll更新所有边的残余流量(即正向弧 - l, 反向弧 + l).
重复步骤 2, 当找不到一条增广路的时候, 重复步骤 1, 重新建立层次图, 直到从源点不能到达汇点为止。