协方差与相关系数
这两个用于表示两个随机变量之间的线性关系。
协方差一般来说就是对图中各点之间构成的矩形求面积和的期望。
一般来说,相关系数不为0,则两个变量之间或多或少存在线性关系(正相关或者负相关)。
相关系数等于协方差除以两个随机变量的标准差。
相关系数是协方差去除了的单位之后,可以用来比较不同变量之间关系的强弱。

最大似然估计法
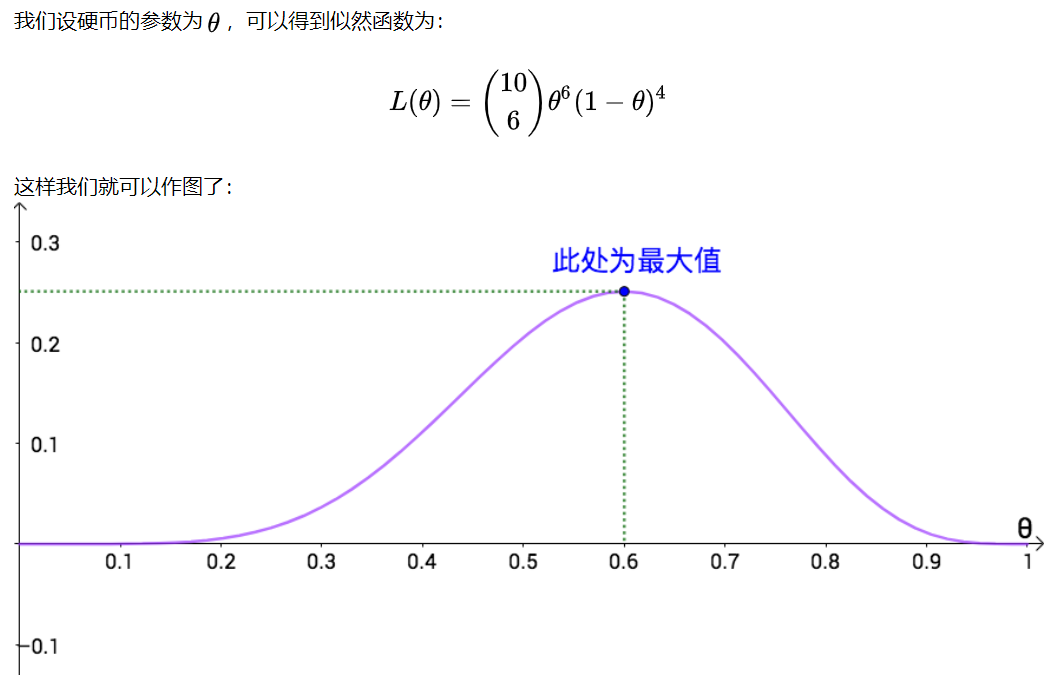
似然,就是通过已知的事实去推测事件概率(参数)的意思。
和贝叶斯推断有相似之处。
例如抛一枚硬币100次,100次正面朝上。
我们可以通过似然函数的极值去推测抛硬币的概率。
最大似然估计法认为,如果事情发生了,那必然是概率最大的。
最小二乘法
即为最小平方法,方差乘以n,记为误差,假设我们用一个函数 ax^2+bx+c 去拟合一些数据,
我们需要使误差最小,误差最小可以使得函数越精准,通过求微积分使误差函数最小的方法可以
求得所拟合的函数参数。
概率论中的矩
其中期望就是一阶矩,二阶矩就是方差。

仿射
仿射是原点进行移动.简单来说 ,仿射变换就是线性变换+移动。
PCA 降维
