7-13 地下迷宫探索 (30 分)
地道战是在抗日战争时期,在华北平原上抗日军民利用地道打击日本侵略者的作战方式。地道网是房连房、街连街、村连村的地下工事,如下图所示。
我们在回顾前辈们艰苦卓绝的战争生活的同时,真心钦佩他们的聪明才智。在现在和平发展的年代,对多数人来说,探索地下通道或许只是一种娱乐或者益智的游戏。本实验案例以探索地下通道迷宫作为内容。
假设有一个地下通道迷宫,它的通道都是直的,而通道所有交叉点(包括通道的端点)上都有一盏灯和一个开关。请问你如何从某个起点开始在迷宫中点亮所有的灯并回到起点?
输入格式:
输入第一行给出三个正整数,分别表示地下迷宫的节点数(,表示通道所有交叉点和端点)、边数(,表示通道数)和探索起始节点编号(节点从1到编号)。随后的行对应条边(通道),每行给出一对正整数,分别是该条边直接连通的两个节点的编号。
输出格式:
若可以点亮所有节点的灯,则输出从开始并以结束的包含所有节点的序列,序列中相邻的节点一定有边(通道);否则虽然不能点亮所有节点的灯,但还是输出点亮部分灯的节点序列,最后输出0,此时表示迷宫不是连通图。
由于深度优先遍历的节点序列是不唯一的,为了使得输出具有唯一的结果,我们约定以节点小编号优先的次序访问(点灯)。在点亮所有可以点亮的灯后,以原路返回的方式回到起点。
输入样例1:
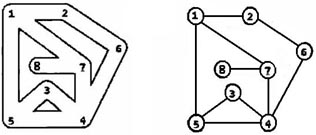
6 8 1 1 2 2 3 3 4 4 5 5 6 6 4 3 6 1 5
输出样例1:
1 2 3 4 5 6 5 4 3 2 1
输入样例2:
6 6 6 1 2 1 3 2 3 5 4 6 5 6 4
输出样例2:
6 4 5 4 6 0
#include<bits/stdc++.h>
using namespace std;
int n,m,s;
int vis[2123]={0};
int tu[3443][3434]={0};
vector<int>o;
int cur;
void dfs(int s){
vis[s]= 1;
cur--;
o.push_back(s);
for(int i=1;i<=n;i++){
if(!vis[i]&&tu[s][i]){
dfs(i);
o.push_back(s);
}
}
}
int main()
{
cin>>n>>m>>s;
for(int i=1;i<=m;i++){
int a,b;
cin>>a>>b;
tu[a][b]= 1;
tu[b][a]= 1;
}
cur = n;
dfs(s);
if(cur!=0){
for(int p:o){
printf("%d ",p);
}
printf("0\n");
}
else{
for(int p:o){
printf("%d ",p);
}
}
}